NLPQLP

Example: 1 % noise level added to the model functions of TP376

Source: Second test problem collection (K. Schittkowski : Nonlinear Programming Codes - Information, Tests, Performance, Lecture Notes in Economics and Mathematical Systems, Vol. 183, Springer, 1980)

Relative Noise: 1 %

Objective Function:

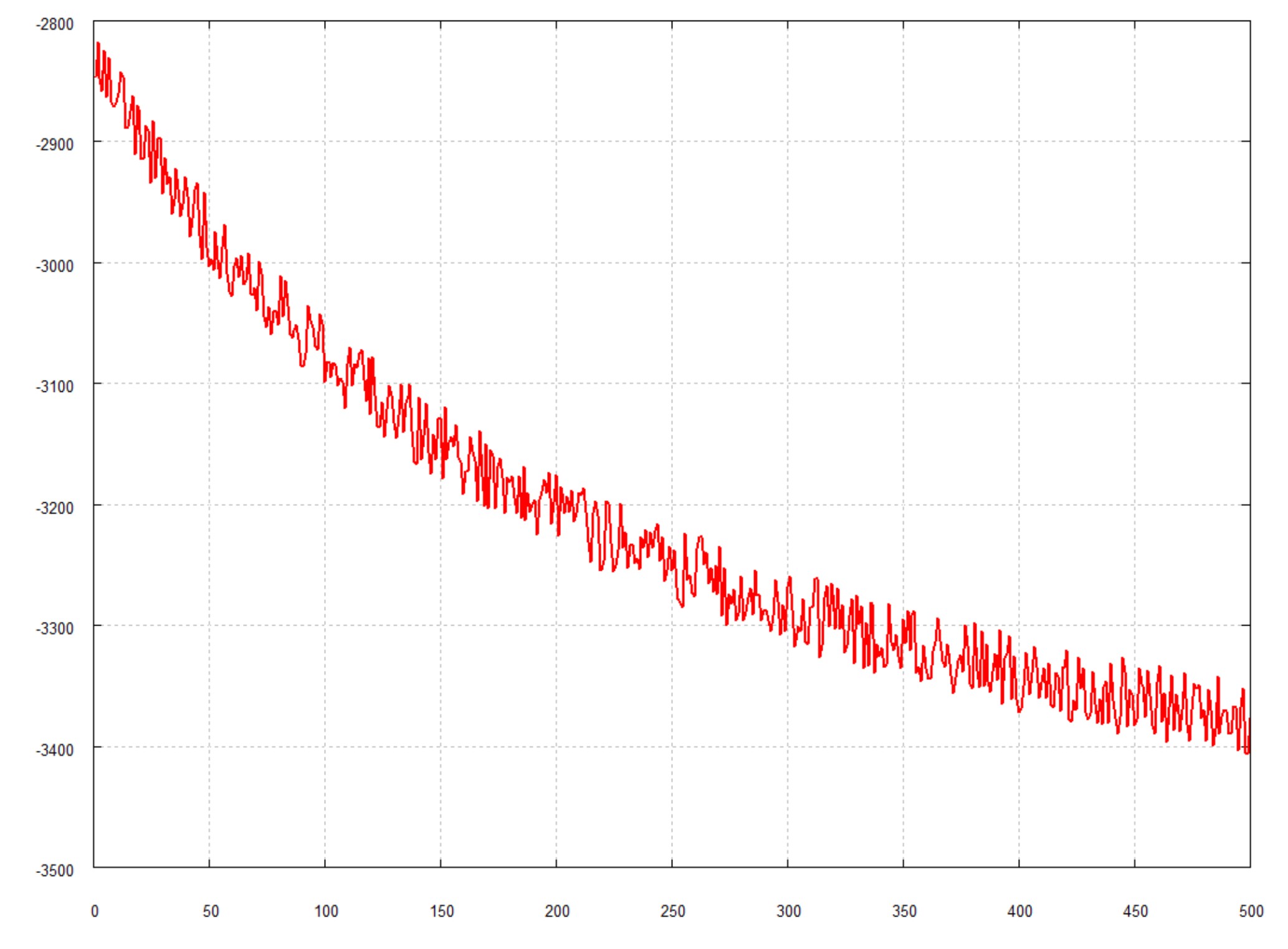
First Partial Derivative: Forward differences

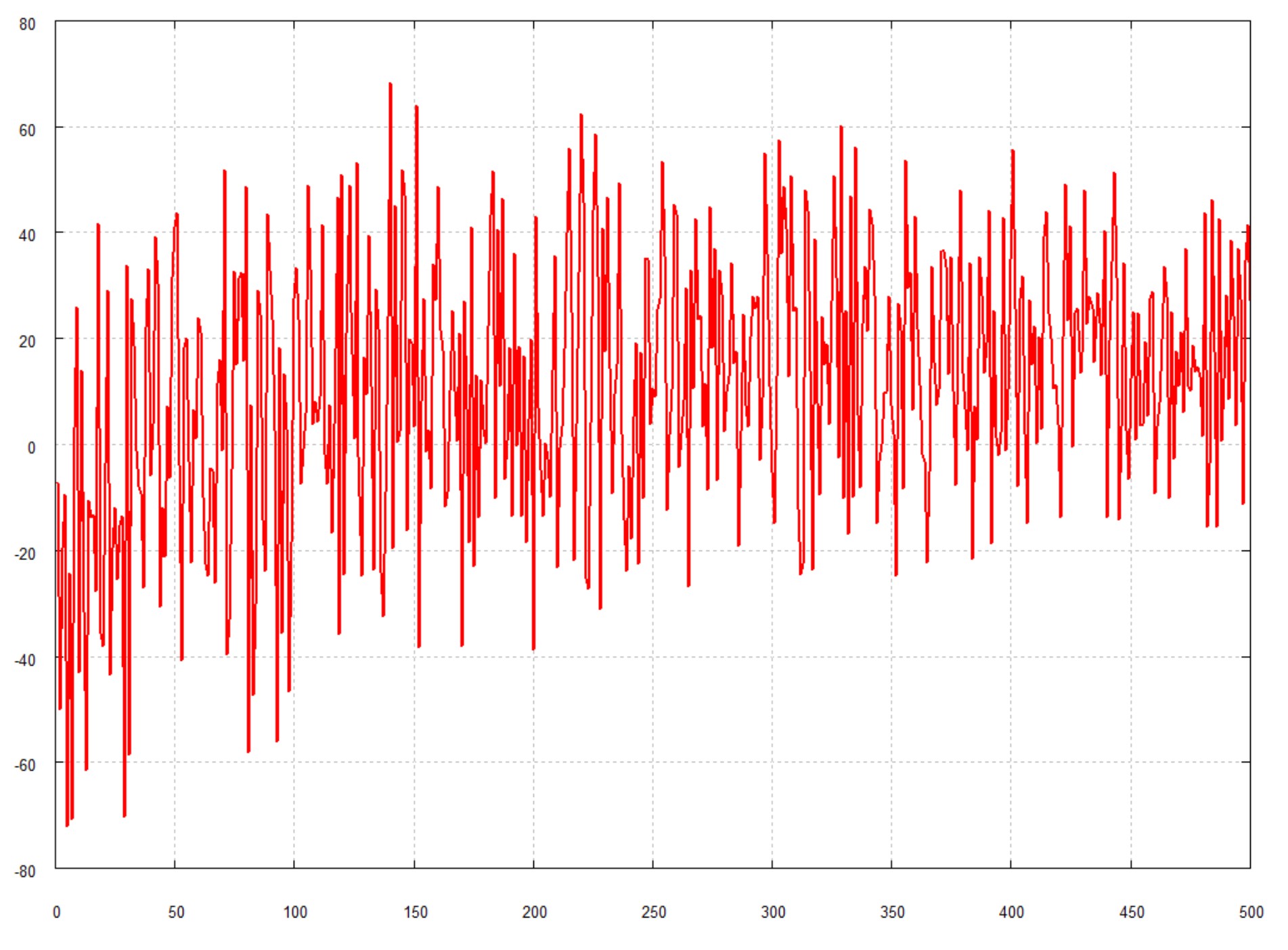
Printout of NLPQLP:

--------------------------------------------------------------------
START OF THE SEQUENTIAL QUADRATIC PROGRAMMING ALGORITHM
--------------------------------------------------------------------
Parameters:
N = 10
M = 15
ME = 1
MODE = 0
ACC = 0.1000D-06
ACCQP = 0.1000D-11
STPMIN = 0.1000D-09
RHOB = 0.1000D+05
MAXFUN = 20
MAXNM = 40
MAXIT = 500
IPRINT = 2

Output in the following order:
IT - iteration number
F - objective function value
SCV - sum of constraint violations
NA - number of active constraints
I - number of line search iterations
ALPHA - steplength parameter
DELTA - additional variable to prevent inconsistency
KKT - Karush-Kuhn-Tucker optimality criterion

IT F SCV NA I ALPHA DELTA KKT
--------------------------------------------------------------------
1 -0.24381779D+04 0.27D-08 15 0 0.00D+00 0.00D+00 0.15D+05
2 -0.35495565D+04 0.41D+02 2 1 0.10D+01 0.00D+00 0.80D+02
3 -0.35630981D+04 0.15D+02 3 1 0.10D+01 0.00D+00 0.61D+04
4 -0.35730489D+04 0.82D+02 3 1 0.10D+01 0.00D+00 0.29D+05
5 -0.35849352D+04 0.13D-02 3 1 0.10D+01 0.00D+00 0.19D+03
6 -0.36198062D+04 0.87D+01 3 1 0.10D+01 0.00D+00 0.46D+03
7 -0.35997493D+04 0.50D+01 5 1 0.10D+01 0.00D+00 0.62D+04
8 -0.35157785D+04 0.33D+02 4 1 0.10D+01 0.00D+00 0.42D+05
9 -0.35337983D+04 0.43D-03 2 1 0.10D+01 0.00D+00 0.34D+03
10 -0.35798137D+04 0.42D-03 3 4 0.25D-01 0.00D+00 0.12D+03
*** INFO: Starting non-monotone line search
11 -0.36028227D+04 0.16D-02 1 1 0.10D+01 0.00D+00 0.12D+03
12 -0.36249683D+04 0.15D-02 2 2 0.10D+00 0.00D+00 0.49D+03
13 -0.36290526D+04 0.15D-02 3 3 0.22D-01 0.00D+00 0.75D+03
14 -0.36461195D+04 0.13D-02 4 2 0.10D+00 0.00D+00 0.35D+03
15 -0.36823974D+04 0.75D-03 4 2 0.41D+00 0.00D+00 0.49D+03
16 -0.37058687D+04 0.66D-03 6 2 0.10D+00 0.00D+00 0.49D+03
17 -0.37067207D+04 0.60D-03 6 2 0.10D+00 0.00D+00 0.48D+03
18 -0.37676416D+04 0.56D-03 6 2 0.10D+00 0.00D+00 0.47D+03
19 -0.37686413D+04 0.56D-03 6 8 0.15D-06 0.00D+00 0.48D+03
20 -0.37748330D+04 0.51D-03 6 2 0.10D+00 0.00D+00 0.74D+03
21 -0.37770724D+04 0.51D-03 6 10 0.11D-07 0.00D+00 0.23D+02
22 -0.37787095D+04 0.51D-03 6 9 0.23D-07 0.00D+00 0.20D+02
23 -0.37811846D+04 0.51D-03 6 14 0.11D-12 0.00D+00 0.20D+01
24 -0.37809565D+04 0.50D-03 6 10 0.12D-08 0.00D+00 0.75D+00
25 -0.37812315D+04 0.46D-03 6 2 0.10D+00 0.00D+00 0.15D+01
26 -0.37831615D+04 0.46D-03 6 14 0.10D-12 0.00D+00 0.12D+01
*** INFO: Starting non-monotone line search
27 -0.37431145D+04 0.19D+01 2 1 0.10D+01 0.00D+00 0.55D+11
28 -0.30536688D+04 0.16D+02 3 1 0.10D+01 0.10D+01 0.20D+12
29 -0.34673526D+04 0.14D+02 3 2 0.48D+00 0.96D+00 0.32D+12
30 -0.36817997D+04 0.90D+03 4 1 0.10D+01 0.10D+01 0.37D+12
31 -0.36962576D+04 0.89D+01 3 2 0.50D+00 0.10D+01 0.30D+12
32 -0.37345485D+04 0.89D-01 2 2 0.26D+00 0.00D+00 0.15D+12
33 -0.37554702D+04 0.25D-02 2 1 0.10D+01 0.00D+00 0.45D+07
34 -0.37162170D+04 0.81D-05 1 1 0.10D+01 0.00D+00 0.31D-01
35 -0.37710564D+04 0.96D-07 1 1 0.10D+01 0.00D+00 0.11D-01
36 -0.37718667D+04 0.96D-07 1 18 0.10D-16 0.00D+00 0.26D-01
37 -0.37720021D+04 0.97D-07 1 10 0.10D-08 0.00D+00 0.98D-02
*** INFO: Starting non-monotone line search
38 -0.37211188D+04 0.84D-08 1 1 0.10D+01 0.00D+00 0.27D-01
39 -0.37435725D+04 0.71D-08 1 1 0.10D+01 0.00D+00 0.39D-02
40 -0.37638656D+04 0.63D-08 1 2 0.10D+00 0.00D+00 0.37D-01
41 -0.37708773D+04 0.25D-08 1 1 0.10D+01 0.00D+00 0.20D-02
42 -0.37735184D+04 0.25D-08 1 9 0.10D-07 0.00D+00 0.71D-02
*** INFO: Starting non-monotone line search
43 -0.37761740D+04 0.15D-10 1 1 0.10D+01 0.00D+00 0.24D-03
*** INFO: Starting non-monotone line search
44 -0.37257254D+04 0.32D-09 1 1 0.10D+01 0.00D+00 0.26D-03
45 -0.37286604D+04 0.11D-09 1 1 0.10D+01 0.00D+00 0.16D-02
46 -0.37344181D+04 0.10D-09 1 3 0.10D-01 0.00D+00 0.10D-01
*** ERROR 2: Search direction not profitable: D*B*D = -0.4523D-04
*** INFO: Restart with rho*I in case of IFAIL=2
48 -0.37647505D+04 0.49D-08 1 1 0.10D+01 0.00D+00 0.46D+02
49 -0.37677198D+04 0.55D-06 1 3 0.10D-01 0.00D+00 0.95D+01
50 -0.37731728D+04 0.54D-06 1 12 0.10D-10 0.00D+00 0.18D+02
51 -0.37741390D+04 0.54D-06 1 7 0.10D-05 0.00D+00 0.40D+03
*** INFO: Starting non-monotone line search
52 -0.37851658D+04 0.14D+02 3 1 0.10D+01 0.48D+00 0.73D+06
53 -0.36523483D+04 0.16D-02 3 1 0.10D+01 0.00D+00 0.89D+03
54 -0.36252736D+04 0.34D-03 4 2 0.30D+00 0.00D+00 0.72D+02
55 -0.36518642D+04 0.74D-04 2 1 0.10D+01 0.00D+00 0.87D+01
56 -0.36704731D+04 0.79D-04 2 3 0.28D-01 0.00D+00 0.47D+00
57 -0.36844420D+04 0.78D-04 2 7 0.10D-05 0.00D+00 0.67D+02
58 -0.36933352D+04 0.11D-03 2 2 0.23D+00 0.00D+00 0.70D+02
59 -0.36969817D+04 0.11D-03 2 8 0.52D-06 0.00D+00 0.37D+01
60 -0.36986348D+04 0.11D-03 2 7 0.10D-05 0.00D+00 0.46D+01
*** INFO: Starting non-monotone line search
61 -0.36796310D+04 0.50D-06 1 1 0.10D+01 0.00D+00 0.46D-02
62 -0.36981323D+04 0.16D-07 2 1 0.10D+01 0.00D+00 0.92D-02
*** INFO: Starting non-monotone line search
63 -0.36629707D+04 0.44D-07 1 1 0.10D+01 0.00D+00 0.15D+01
64 -0.36766726D+04 0.12D-05 2 2 0.10D+00 0.00D+00 0.21D-02
65 -0.36978662D+04 0.11D-05 2 5 0.10D-03 0.00D+00 0.15D+00
*** INFO: Starting non-monotone line search
66 -0.36909664D+04 0.19D-05 1 1 0.10D+01 0.00D+00 0.16D+00
67 -0.36980467D+04 0.19D-05 2 5 0.10D-03 0.00D+00 0.63D+01
*** INFO: Starting non-monotone line search
68 -0.36841253D+04 0.98D-05 2 1 0.10D+01 0.00D+00 0.79D-01
69 -0.36877924D+04 0.87D-05 2 2 0.10D+00 0.00D+00 0.81D-01
70 -0.36925197D+04 0.78D-05 2 2 0.10D+00 0.00D+00 0.20D+00
71 -0.36974763D+04 0.56D-06 2 1 0.10D+01 0.00D+00 0.28D-02
*** INFO: Starting non-monotone line search
72 -0.36799515D+04 0.76D-08 2 1 0.10D+01 0.00D+00 0.49D-02
73 -0.36822846D+04 0.75D-08 2 5 0.10D-03 0.00D+00 0.21D+00
74 -0.36909392D+04 0.21D-05 2 1 0.10D+01 0.00D+00 0.16D+00
75 -0.36930425D+04 0.19D-05 2 2 0.10D+00 0.00D+00 0.41D+00
76 -0.36976898D+04 0.19D-05 2 16 0.10D-14 0.00D+00 0.98D-01
*** INFO: Starting non-monotone line search
77 -0.36905618D+04 0.16D-07 1 1 0.10D+01 0.00D+00 0.19D-03
78 -0.36962132D+04 0.16D-07 1 5 0.10D-03 0.00D+00 0.23D-02
*** INFO: Starting non-monotone line search
79 -0.36390775D+04 0.31D-08 2 1 0.10D+01 0.00D+00 0.84D-03
80 -0.36422286D+04 0.33D-09 1 1 0.10D+01 0.00D+00 0.40D-04
81 -0.36493805D+04 0.30D-09 1 2 0.10D+00 0.00D+00 0.43D-04
82 -0.36726372D+04 0.29D-09 1 3 0.10D-01 0.00D+00 0.55D-03
83 -0.36773766D+04 0.29D-09 1 7 0.10D-05 0.00D+00 0.25D-04
84 -0.36897748D+04 0.29D-09 1 5 0.10D-03 0.00D+00 0.14D-04
85 -0.36934605D+04 0.29D-09 1 3 0.10D-01 0.00D+00 0.73D-04
86 -0.36968038D+04 0.29D-09 1 7 0.10D-05 0.00D+00 0.67D-04
*** INFO: Starting non-monotone line search
87 -0.36912671D+04 0.53D-09 1 1 0.10D+01 0.00D+00 0.36D-05
88 -0.36974576D+04 0.14D-10 1 1 0.10D+01 0.00D+00 0.58D-04
89 -0.37011275D+04 0.14D-10 1 7 0.10D-05 0.00D+00 0.12D-05
*** INFO: Starting non-monotone line search
90 -0.36694167D+04 0.29D-11 1 1 0.10D+01 0.00D+00 0.33D-07

--- Final Convergence Analysis at Last Iterate ---

Objective function value: F(X) = -0.36694167D+04
Solution values: X =
0.72179618D+01 0.10000000D+00 0.25074957D-02 0.94117926D+03
0.50000000D-04 0.14397846D-03 0.26876699D-02 0.50368280D-04
0.20383513D+00 0.51164868D-01
Distances from lower bounds: X-XL =
0.72179618D+01 0.10000000D+00 0.24574957D-02 0.93117926D+03
0.00000000D+00 0.93978457D-04 0.26376699D-02 0.36828002D-06
0.20378513D+00 0.51114868D-01
Distances from upper bounds: XU-X =
0.27820382D+01 0.00000000D+00 0.55925043D-02 0.58820742D+02
0.16500000D-02 0.11560215D-02 0.12330108D-04 0.19496317D-02
0.79616487D+00 0.94883513D+00
Multipliers for lower bounds: U =
0.00000000D+00 0.00000000D+00 0.00000000D+00 0.00000000D+00
0.95772448D+03 0.00000000D+00 0.00000000D+00 0.00000000D+00
0.00000000D+00 0.00000000D+00
Multipliers for upper bounds: U =
0.00000000D+00 0.32079605D+04 0.00000000D+00 0.00000000D+00
0.00000000D+00 0.00000000D+00 0.00000000D+00 0.00000000D+00
0.00000000D+00 0.00000000D+00
Constraint values: G(X) =
-0.28710178D-11 0.69174651D+01 0.28897889D+01 0.68806532D+01
0.71278782D+01 0.45689515D+01 0.99559270D+03 0.10012153D+04
0.99190875D+03 0.99135239D+03 0.10070953D+04 0.99611216D+03
0.98276046D+03 0.10064607D+04 0.14387129D+02
Multipliers for constraints: U =
-0.92227688D+02 0.00000000D+00 0.00000000D+00 0.00000000D+00
0.00000000D+00 0.00000000D+00 0.00000000D+00 0.00000000D+00
0.00000000D+00 0.00000000D+00 0.00000000D+00 0.00000000D+00
0.00000000D+00 0.00000000D+00 0.00000000D+00
Number of function calls: NFUNC = 605
Number of gradient calls: NGRAD = 89
Number of calls of QP solver: NQL = 95

References:

	Yu-hong Dai, K. Schittkowski (2008): A sequential quadratic programming algorithm with non-monotone line search, Pacific Journal of Optimization, Vol. 4, 335-351
	K. Schittkowski, NLPQLP: A Fortran implementation of a sequential quadratic programming algorithm with distributed and non-monotone line Search - User's guide, Version 3.0, Report, Department of Computer Science, University of Bayreuth (2009)
	K. Schittkowski, NLPQL: A Fortran subroutine for solving constrained nonlinear programming problems, Annals of Operations Research, Vol. 5, 485-500 (1985/86)
	K. Schittkowski (2010): A robust implementation of a sequential quadratic programming algorithm with successive error restoration, submitted for publication
	K. Schittkowski (1987): More Test Examples for Nonlinear Programming, Lecture Notes in Economics and Mathematical Systems, Vol. 282, Springer

Availability:
For more details contact the author or click here for free license for members and students of academic institutions.

Back to home page	Back to list of software	klaus@schittkowski.de